Страница: 3/5
Тем более, если рассматривать величину Т и величину В (возраст хирурга), то данные величины практически независимы.
До сих пор мы обсуждали свойства систем случайных величин, давая только словесное разъяснение. Однако существуют числовые характеристики, посредством которых исследуются свойства как отдельных случайных величин, так и системы случайных величин.
Одной из важнейших характеристик случайной величины нормального распределения является математическое ожидание.
Рассмотрим дискретную случайную величину Х, имеющую возможные значения Х1, Х2, . , Хn с вероятностями р1, р2, . , рn. нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные значения. Для этой цели обычно пользуются так называемым "средним взвешенным" из значений Хi, причем каждое значение Хi при осреднении должно учитываться с "весом", пропорциональным вероятности этого значения. Таким образом, если обозначить "среднее взвешенное" через М[X] или mx, получим
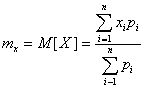
или, учитывая, что 
, то
(1).
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Для большей наглядности рассмотрим одну механическую интерпретацию введенного понятия. Пусть на оси абсцисс расположены точки с абсциссами х1, х2, …, хn, в которых сосредоточены соответственно массы р1, р2, … , рn, причем . Тогда математическое ожидание есть не что иное, как абсцисса центра тяжести данной системы материальных точек.
Формула (1) для математического ожидания соответствует случаю дискретной случайной величины. Для непрерывной величины Х математическое ожидание, естественно, выражается не суммой, а интегралом:
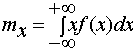
(2),
где 
- плотность распределения величины Х.
Формула (2) получается из формулы (1), если в ней заменить отдельные значения Хi непрерывно изменяющимся параметром Х, соответствующие вероятности рi элементом вероятности f(x)dx, конечную сумму - интегралом.
В механической интерпретации математическое ожидание непрерывной случайной величины сохраняет тот же смысл - абсциссы центра тяжести в случае, когда масса распределения по оси абсцисс непрерывна с плотностью f(x).
Следует отметить, что математическое ожидание существует не для всех случайных величин, что, однако, по мнению некоторых ученых, не представляет для практики существенного интереса.
Помимо математического ожидания важное значение имеют также другие числовые случайной величины - моменты.
Понятие момента широко применяется в механике для описания распределения масс ( статистические моменты, моменты инерции и т.д.). Совершенно теми же приемами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.
Начальным моментом s-го порядка прерывной случайной величины Х называется сумма вида
Очевидно это определение совпадает с определением начального момента порядка s в механике, если на оси абсцисс в точках х1, …, хn сосредоточена масса р1, …, рn.
Для непрерывной случайной величины Х начальным моментом s-го порядка называется интеграл
Очевидно, что
,
т.е. начальный момент s-го порядка случайной величины Х есть не что иное, как математическое ожидание s-ой степени этой случайной величины.
Перед тем как дать определение центрального момента введем понятие "центрированной случайной величины".
Пусть имеется случайная величина Х с математическим ожиданием mx. Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания
Нетрудно видеть, что математическое ожидание центрированной случайной величины равно нулю.
Центрирование случайной величины равносильно переносу начала координат в точку, абсцисса которой равна математическому ожиданию.
Реферат опубликован: 7/07/2008